Daniel Brod (UFF Niteroi): (Bipartite) Gaussian Boson Sampling
Quantum Information and Quantum Computing Seminars CTP PAS 2022-01-26
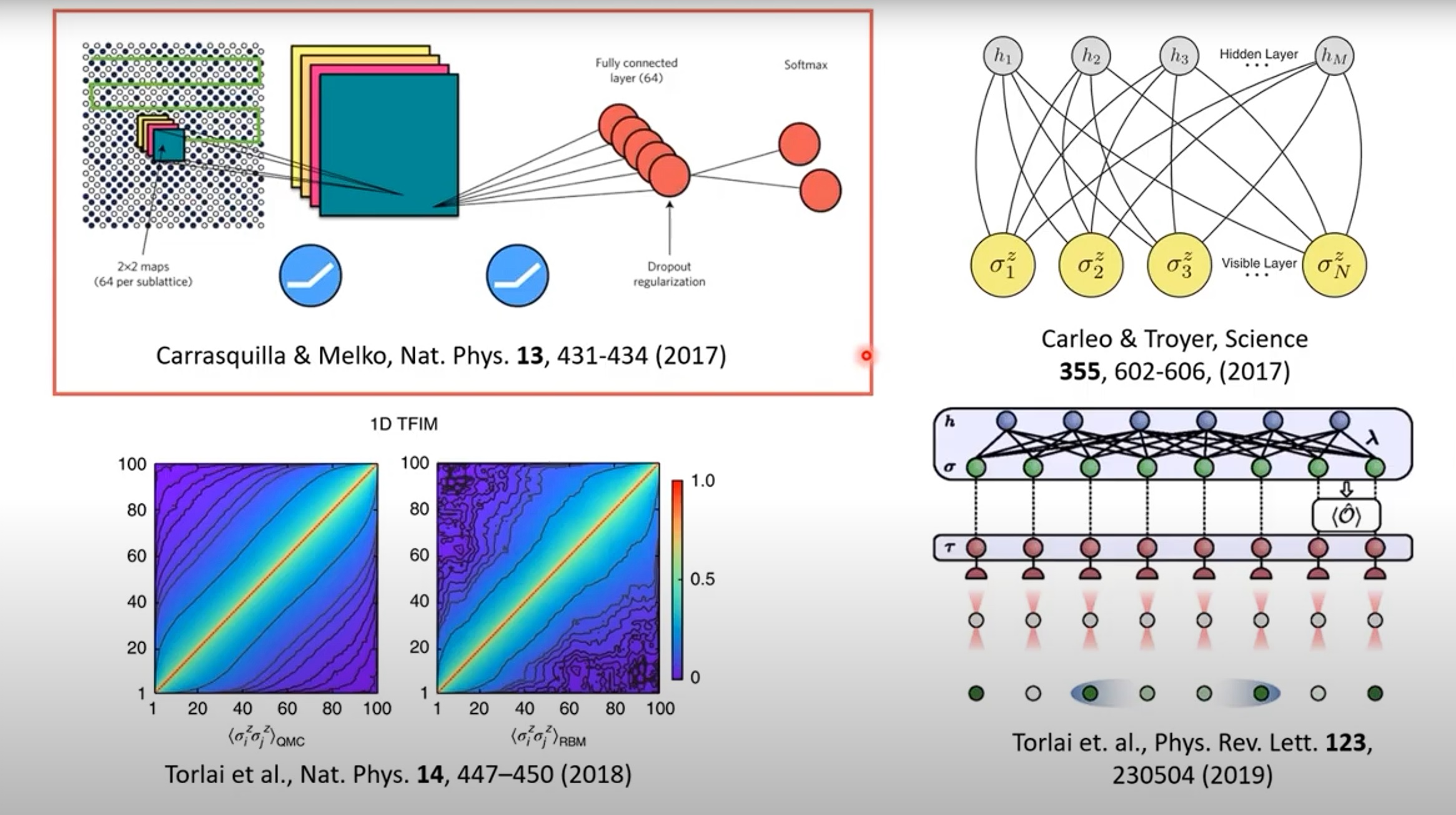
Gaussian Boson Sampling. Gaussian boson sampling is a model of photonic quantum computing that has attracted attention as a platform for quantum devices capable of performing tasks that are out of reach of their classical counterparts. Most recent photonic quantum computational advantage experiments were performed within this Gaussian variant of boson sampling, having observed events with over 100 photons and seriously challenged the capabilities of competing classical algorithms. Thus, there is significant interest in solidifying the mathematical and complexity-theoretic foundations for the hardness of simulating these devices. We show that there is no efficient classical algorithm to approximately sample from the output of an ideal Gaussian boson sampling device unless the polynomial hierarchy collapses, under the same two conjectures as the original boson sampling proposal by Aaronson and Arkhipov. Crucial to the proof is a new method for programming a Gaussian boson sampling device such that the output probabilities are proportional to permanents of (submatrices of) an arbitrary matrix. This provides considerable flexibility in programming, and likely has applications much beyond those discussed here. We leverage this to make progress towards the goal of proving hardness in the regime where there are fewer than quadratically more modes than photons (i.e., in the high-collision regime). Our reduction suffices to prove that GBS is hard in the constant-collision regime, though we believe some ingredients of it can be used to push this direction further.
Other seminars

Giulio Chiribella (University of Hong Kong): Optimal programming of quantum gates - Duplicate27-06-2022

Marco Tomamichel (National University of Singapore): Quantum advantage with noisy shallow circuits17-05-2022

R. Patron (University of Edinburgh): Limitations of optimization algorithms on noisy quantum devices02-03-2022

Marcel Hinsche (FU Berlin): Learnability of the output distributions of local quantum circuits25.05.2022

Julio de Vicente: Genuine multipartite entanglement and nonlocality in pair-entangled network states20.04.2022

Beata Zjawin (ICTQT): Inequality Constraints in Directed Acyclic Graphs with Hidden Variables02.02.2022

Laura Mancinska (QMATH, Copenhagen): Fixed-size schemes for certification of large quantum systems17-11-2021
Yelena Guyanova (IQOQI, Vienna): Ideal Projective Measurements Have Infinite Resource Costs10-11-2021

Hamed Mohammady (ULdB): Measurement disturbance and conservation laws in quantum mechanics03-11-2021